Karmaşık sayılar kümesi birçok şekilde tanımlanabilir. Aşağıdaki tanımların hepsi birbirine eşyapısaldır, yani yapısal olarak biri diğerinin yerine kullanılabilir. Bu yüzden aslında içerik olarak farklı olan aşağıda tanımlanan tüm kümeleri aynı harfle gösterdik,
 . Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.
. Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.Kartezyen uzay tanımı [değiştir]
Gerçel sayılar kümesinde her sayıyı ile çarparsak elde ettiğimiz
ile çarparsak elde ettiğimiz  kümesi önceki
kümesi önceki  kümesine eşyapısaldır. Karmaşık sayılar cismi ise buradan hareketle
kümesine eşyapısaldır. Karmaşık sayılar cismi ise buradan hareketle yerine tamsayılar cismi
yerine tamsayılar cismi  alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.
alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.Karmaşık sayılar, bu tanımla aşağıdaki gibi ifade edilir:
 olmak üzere;
olmak üzere; ve
ve  dir.
dir.Cisim genişlemesi tanımı [değiştir]
Karmaşık olmayan sayılar, gerçel sayılar cisminin bir cisim genişlemesidir. sayısı
sayısı  polinomunun köklerinden biridir ve diğer kökü de
polinomunun köklerinden biridir ve diğer kökü de  olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşcyapısal olduğu kolaylıkla görülebilir:
olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşcyapısal olduğu kolaylıkla görülebilir: polinomuyla üretilen bölüm halkasıdır:
polinomuyla üretilen bölüm halkasıdır: karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının
karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının  olarak ifade edildiği bu tanıma daha âşinâyız.
olarak ifade edildiği bu tanıma daha âşinâyız.Karmaşık düzlem [değiştir]
İşlemlerin geometriksel açıklaması [değiştir]
Cebirsel olarak ifade edilen işlemler yukarıdaki karmaşık düzlem kullanılarak gösterilebilir. | X = A + B: Karmaşık düzlemdeki A ve B gibi iki noktanın 'toplamı, X = A + Bdir ve köşeleri 0,A, B olan bir üçgendir. X, B, A ile benzerdir. Bu iki karmaşık sayı, vektör uzayında aynı katkıya sahiptir. |
 | X = AB: A ve B gibi iki noktanın çarpımı X = ABdir ve köşeleri 0, 1, A olan bir üçgendir. 0, B, X benzer üçgenlerdir. |
 | X = A*: A noktasının Karmaşık eşleniği, X = A*dır ve köşeleri 0, 1, Adır. 0, 1, Xnin ayna görüntüsüdür. |


fonksiyonunun alan renklendirme çizimi. Ton, fonksiyon değişkenini ifade ederken, doygunluk ve canlılık miktarı ifade eder.
Kutupsal form [değiştir]
Şablon:Detail olarak yazılır. Pisagor teoremine göre,
olarak yazılır. Pisagor teoremine göre, fonksiyonu ile gösterilir. Bu fonksiyon, karmaşık sayıların metrik uzayına dönüşüdür. Limit ve süreklilik hakkında fikir verir. İki boyutlu uzayın tüm standart özellikleri karmaşık sayılar için geçerlidir. (tüm z ve w için,
fonksiyonu ile gösterilir. Bu fonksiyon, karmaşık sayıların metrik uzayına dönüşüdür. Limit ve süreklilik hakkında fikir verir. İki boyutlu uzayın tüm standart özellikleri karmaşık sayılar için geçerlidir. (tüm z ve w için,  ).
).İkinci olarak,
 şeklindeki karmaşık sayının argümanı veya fazı, reel eksenle yaptığı açıdır (Şekil 2'de φ olarak gösteriliyor) ve
şeklindeki karmaşık sayının argümanı veya fazı, reel eksenle yaptığı açıdır (Şekil 2'de φ olarak gösteriliyor) ve  olarak yazılır. Mutlak değer olarak, argüman dikdörtgensel formdan elde edilebilir
olarak yazılır. Mutlak değer olarak, argüman dikdörtgensel formdan elde edilebilir  :
: veya
veya  (
( olduğunda π ekleyerek,
olduğunda π ekleyerek,  olur).
olur).
![(-\pi,\pi]](http://upload.wikimedia.org/wikipedia/tr/math/f/c/f/fcfe3f8f790d9246dce2f4e70705730f.png) veya
veya  aralığında seçilir (Bu asıl değerdir).
aralığında seçilir (Bu asıl değerdir).Karmaşık sayıların çeşitli formlarda gösterilebilir. Kutupsal form, bir düzlemdeki noktanın tam konumunu belirten mutlak değer ve argüman bileşenleri olarak gösterilebilir, şöyle ki; (r,φ) kutupsal çiftlerinden, özgün dikdörtgenin koordinatları olan
 elde edildi). Diğer gösterimi:
elde edildi). Diğer gösterimi:Kutupsal formdaki işlemler [değiştir]
Çarpma ve bölme kutupsal formda temel formüllere sahiptir: ), bunlar aynı ifade altına alınırken çarpma işleminde üsler toplanır, bölme işleminde ise üsler çıkartılır.
), bunlar aynı ifade altına alınırken çarpma işleminde üsler toplanır, bölme işleminde ise üsler çıkartılır.Üs tam sayı ise şöyle gösterilir:
Sonuç olarak kutupsal formlar kökleri bulmak içinde kullanılabilir. z herhangi karmaşık sayı olmak üzere ve n pozitif tam sayı için zn = c olarak gösterilebilir. Bu da cnin n. kökü diye okunur. Eğer c sıfır değilse, tam n tane farklı c nin kökü vardır (cebirin temel teoremine göre). r > 0 için, c = re iφ'de c nin n. kökleri:
![\sqrt[n]{r}](http://upload.wikimedia.org/wikipedia/tr/math/0/c/1/0c1dda2d990c60ca5ef80cd446e594db.png) , pozitif reel sayı olan r nin genellikle pozitif olan n. kökünü ifade eder. Eğer c = 0, ise c nin tek bir kökü vardır, o da 0'dır.
, pozitif reel sayı olan r nin genellikle pozitif olan n. kökünü ifade eder. Eğer c = 0, ise c nin tek bir kökü vardır, o da 0'dır.Karmaşık sayılarda işlem [değiştir]
Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir. Öncelikle iki karmaşık sayının eşitliğini verelim.Eşitlik [değiştir]
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları için ancak
ancak  ve
ve  iken geçerlidir.bu doğru bir kavramdır...
iken geçerlidir.bu doğru bir kavramdır...
Toplama [değiştir]
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları içinÇarpma [değiştir]
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları içinEşlenik [değiştir]
Bir karmaşık sayısı için eşlenik ifadesi
karmaşık sayısı için eşlenik ifadesi  dönüşümüdür ve
dönüşümüdür veEşleniğin cebirsel özellikleri [değiştir]




 ancak z gerçel sayı olduğunda geçerlidir.
ancak z gerçel sayı olduğunda geçerlidir.
Çarpımsal Ters [değiştir]
Bir karmaşık sayısının tersi ancak
karmaşık sayısının tersi ancak



![\mathbb{C} \equiv \mathbb{R} [ X ] / (X^2+1) \equiv \{ \, a + \mathbf{i} b \, | \, a,b \in \mathbb{R} \, \}](http://upload.wikimedia.org/wikipedia/tr/math/5/e/7/5e70f934a2e936b63f0798d6b0092153.png)

 (veya
(veya  olarak ta gösterilir) dikdörtgendir ve noktayı ifade eder.
olarak ta gösterilir) dikdörtgendir ve noktayı ifade eder.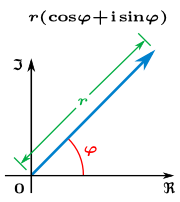
 veya
veya  .
.






![\left\{ \sqrt[n]r\,e^{i\left(\frac{\varphi+2k\pi}{n}\right)} \mid k\in\{0,1,\ldots,n-1\} \, \right\}](http://upload.wikimedia.org/wikipedia/tr/math/c/d/e/cde35c4970fef7c762412dfea38c399a.png)







Hiç yorum yok:
Yorum Gönder